Mekanika Kuantum
- Untuk me nyelesaikan tugas kimia yg diberi oleh bapak Darwison,M.t
- Untuk memahami materi mengenai mekanika kuantum
- Bilangan Kuantum
- Magnet
- Elektron
Werner Heisenberg merumuskan apa yang sekarang dikenal sebagai prinsip ketidakpastian Heisenberg, tidak mungkin untuk mengetahui secara bersamaan kedua momentum p (didefinisikan sebagai massa kali kecepatan) dan posisi suatu partikel dengan pasti. Dinyatakan secara matematis,
di mana 𝛥x dan 𝛥p adalah ketidakpastian dalam mengukur posisi dan momentum partikel, masing-masing. Tanda ≥ memiliki arti sebagai berikut. Jika ketidakpastian posisi dan momentum yang diukur adalah besar (katakanlah, dalam eksperimen kasar), produknya dapat secara substansial lebih besar daripada h/4𝝅 (karenanya tanda >). Signifikansi dari Persamaan 7.9 adalah bahwa bahkan dalam kondisi yang paling menguntungkan untuk mengukur posisi dan momentum, produk dari ketidakpastian tidak pernah dapat kurang dari h/4𝝅 (karenanya tanda =). Dengan demikian, membuat pengukuran momentum suatu partikel lebih tepat (yaitu, membuat 𝛥p dalam jumlah kecil) berarti bahwa posisi tersebut harus menjadi kurang tepat (yaitu, 𝛥x akan menjadi lebih besar). Demikian pula, jika posisi partikel diketahui lebih tepat, pengukuran momentumnya harus menjadi kurang tepat.
Menerapkan prinsip ketidakpastian Heisenberg pada atom hidrogen, kita melihat bahwa pada kenyataannya elektron tidak mengorbit inti dalam jalur yang didefinisikan dengan baik. Kita dapat menentukan secara tepat posisi elektron (dari lokasinya pada orbit tertentu) dan momentumnya (dari energi kinetiknya) pada saat yang sama, sebuah pelanggaran terhadap prinsip ketidakpastian.
Bohr memberikan kontribusi yang signifikan bagi pemahaman kita tentang atom, dan sarannya bahwa energi elektron dalam atom dikuantisasi tetap tidak tertandingi. Namun teorinya tidak memberikan deskripsi lengkap tentang perilaku elektronik dalam atom. Pada tahun 1926, fisikawan Austria Erwin Schrödinger, menggunakan teknik matematika, Ia merumuskan persamaan yang menggambarkan perilaku dan energi partikel submikroskopik secara umum, sebuah persamaan yang analog dengan hukum gerak Newton untuk objek makroskopik. Persamaan Schrödinger membutuhkan kalkulus canggih untuk diselesaikan. Persamaan tersebut menggabungkan perilaku partikel, dalam hal massa m, dan perilaku gelombang, dalam hal fungsi gelombang 𝜓 (psi), yang tergantung pada lokasi dalam ruang sistem (seperti sebuah elektron dalam atom).
Gagasan mengaitkan 𝜓² dengan probabilitas berasal dari analogi teori gelombang. Menurut teori gelombang, intensitas cahaya sebanding dengan kuadrat amplitudo gelombang, atau 𝜓². Tempat yang paling mungkin untuk menemukan foton adalah di mana intensitas terbesar, yaitu, di mana nilai 𝜓² terbesar. Argumen serupa mengaitkan 𝜓² dengan kemungkinan menemukan elektron di daerah sekitar inti.
Persamaan Schrödinger membentuk era baru dalam ilmu fisika dan kimia, karena ia meluncurkan sebuah penemuan,yaitu mekanika kuantum (mekanika gelombang).
Deskripsi Mekanika Kuantum dari Atom Hidrogen
Persamaan Schrödinger dapat menentukan keberadaan energi yang dimiliki oleh elektron terhadap atom hidrogen dan dapat mengidentifikasi fungsi gelombang (𝜓). Keadaan energi dan fungsi gelombang ini ditandai oleh sejumlah bilangan kuantum, dengan ini kita dapat membuat model atom hidrogen yang komprehensif.
Meskipun mekanika kuantum tidak dapat menunjukan lokasi elektron dalam atom, tetapi ia dapat menentukan wilayah elektron pada waktu tertentu. Konsep kerapatan elektron memberikan probabilitas bahwa elektron akan ditemukan di wilayah tertentu dari atom. Kuadrat dari fungsi gelombang (𝜓²), merupakan distribusi kerapatan elektron dalam ruang tiga dimensi di sekitar inti. Daerah dengan kerapatan elektron yang tinggi menunjukkan probabilitas yang tinggi untuk menemukan elektron, sedangkan yang sebaliknya berlaku untuk daerah dengan kerapatan elektron yang rendah
Gambar diatas Representasi distribusi kerapatan elektron yang mengelilingi inti atom hidrogen. Ini menunjukkan probabilitas tinggi untuk menemukan elektron lebih dekat ke inti.
Persamaan Schrödinger bekerja dengan baik untuk atom hidrogen sederhana dengan satu proton dan satu elektronnya, tetapi ternyata tidak dapat diselesaikan dengan tepat untuk setiap atom yang mengandung lebih dari satu elektron. Dengan demikian, kita dapat menggunakan energi dan fungsi gelombang yang diperoleh dari atom hidrogen sebagai perkiraan perilaku elektron dalam atom yang lebih kompleks. Faktanya, pendekatan ini memberikan deskripsi perilaku elektronik dalam atom banyak elektron yang cukup andal.
Dalam mekanika kuantum, diperlukan diperlukan tiga bilangan kuantum untuk menggambarkan distribusi elektron terhadap hidrogen dan atom lainnya. Mereka disebut bilangan kuantum utama, bilangan kuantum momentum sudut , dan bilangan kuantum magnetik. Bilangan ini digunakan untuk menggambarkan orbital atom dan memberi label elektron. Bilangan kuantum keempat, yaitu bilangan kuantum spin,menggambarkan perilaku elektron tertentu dan melengkapi deskripsi elektron dalam atom
7.6.1 Bilangan Kuantum Utama (n)
Bilangan kuantum utama (n) dapat memiliki nilai integral 1, 2, 3, dan seterusnya. Dalam atom hidrogen, nilai n menentukan energi orbital. Bilangan kuantum utama juga berkaitan dengan jarak rata-rata elektron dari inti dalam orbital tertentu. Semakin besar n adalah, semakin besar jarak rata-rata elektron dalam orbital dari inti dan karenanya semakin besar orbital.
7.6.2 Bilangan Kuantum Momentum Sudut (ℓ)
Nilai ℓ tergantung pada nilai bilangan kuantum utama, n. Untuk nilai n yang diberikan, ℓ memiliki nilai integral yang mungkin dari 0 hingga (n = ℓ). Jika n = 1, hanya ada satu nilai yang mungkin dari ℓ; yaitu, ℓ = n - 1 = 1 - 1 = 0. Jika n = 2, ada dua nilai ℓ, yang diberikan oleh 0 dan 1. Jika n = 3, ada tiga nilai ℓ, yang diberikan oleh 0, 1 , dan 2. Nilai ℓ umumnya ditentukan oleh huruf s, p, d,. . . sebagai berikut:
Jadi, jika ℓ = 0, kita memiliki orbital s; jika ℓ = 1, kita memiliki orbital p; dan seterusnya.
Kumpulan orbital dengan nilai n yang sama sering disebut kulit. Satu orbital atau lebih dengan nilai n yang sama dan ℓ disebut sebagai subkulit. Misalnya, kulit dengan n = 2 terdiri dari dua subkulit, ℓ = 0 dan 1 (nilai yang diizinkan untuk n = 2). Subkulit ini disebut subkulit 2s dan 2p di mana 2 menunjukkan nilai n, dan s dan p menunjukkan nilai ℓ.
7.6.3 Bilangan Kuantum Magnetik (mℓ)
Dalam subkulit, nilai mℓ tergantung pada nilai bilangan kuantum momentum sudut, ℓ. Untuk nilai tertentu dari ℓ, ada (2ℓ + 1) nilai integral mℓ sebagai berikut:
-ℓ, (-ℓ+1), ...0,...(+ℓ-1), ℓ
Jika ℓ = 0, maka mℓ = 0. Jika ℓ = 1, maka ada [(2 x 1) + 1], atau tiga nilai mℓ, yaitu, -1, 0, dan 1. Jika ℓ = 2, ada [(2 x 2) + 1], atau lima nilai mℓ, yaitu, -2, -1, 0, 1, dan 2. Jumlah mℓ menunjukkan jumlah orbital dalam sebuah subkulit dengan nilai ℓ subkulit tertentu.
7.6.4 Bilangan Kuantum Spin Elektron (ms)
Menurut teori elektromagnetik, muatan berputar menghasilkan medan magnet, dan gerakan inilah yang menyebabkan elektron berperilaku seperti magnet. Gambar dibawah menunjukkan dua gerakan pemintalan yang mungkin dari sebuah elektron, satu searah jarum jam dan lainnya berlawanan arah jarum jam. Untuk memperhitungkan perputaran elektron, kita perlu memasukkan bilangan kuantum keempat, yang disebut bilangan kuantum spin elektron (ms), yang memiliki nilai -½ atau +½.
Pada gambar diatas (a) putaran searah jarum jam dan (b) putaran berlawanan arah jarum jam dari suatu elektron. Medan magnet yang dihasilkan oleh dua gerakan berputar ini analog dengan yang berasal dari dua magnet. Panah ke atas dan ke bawah digunakan untuk menunjukkan arah putaran.
Interaksi antara elektron dan medan magnet menyebabkan atom terdefleksi dari jalur garis lurusnya. Karena gerakan perputaran benar-benar acak, elektron di setengah atom akan berputar dalam satu arah, dan atom-atom itu akan terdefleksi dalam satu cara; elektron-elektron di bagian lain dari atom-atom akan berputar ke arah yang berlawanan, dan atom-atom itu akan terdefleksi ke arah yang lain. Dengan demikian, dua titik dengan intensitas yang sama diamati pada layar pendeteksi.
Tabel dibawah menunjukkan hubungan antara bilangan kuantum dan orbital atom. Kita melihat bahwa ketika 𝓁 = 0, (2𝓁 + 1) = 1 dan hanya ada satu nilai mℓ, maka kita memiliki orbital s. Ketika 𝓁 = 1, (2𝓁 + 1) = 3, maka ada tiga nilai orbital mℓ atau tiga p, berlabel px, py, dan pz. Ketika 𝓁 = 2, (2𝓁 + 1) = 5 dan ada lima nilai mℓ, dan lima orbital yang sesuai diberi label dengan subskrip yang lebih rumit. Pada bagian berikut ini kita akan memperhatikan orbital s, p, dan d secara terpisah.
Hubungan Antara Bilangan Kuantum dan Orbital Atom
Sebenarnya, orbital tidak memiliki bentuk yang terdefinisi dengan baik karena fungsi gelombang yang mencirikan orbital memanjang dari inti hingga tak terbatas. Dalam hal ini, sulit untuk mengatakan seperti apa bentuk orbital itu. Di sisi lain, tentu saja nyaman untuk berpikir bahwa orbital memiliki bentuk tertentu, khususnya dalam membahas pembentukan ikatan kimia antara atom.
Meskipun pada prinsipnya sebuah elektron dapat ditemukan di mana saja, kita tahu bahwa sebagian besar waktu elektron cukup dekat dengan inti. Gambar (a) menunjukkan distribusi kerapatan elektron dalam orbital hidrogen 1s yang bergerak keluar dari inti. Seperti yang Anda lihat, kerapatan elektron turun dengan cepat ketika jarak dari inti meningkat. Secara kasar, ada sekitar 90 persen kemungkinan menemukan elektron dalam radius 100 pm (1 pm = 1 x 10⁻¹² m) yang mengelilingi inti. Dengan demikian, kita dapat mewakili orbital 1s dengan menggambar diagram batas permukaan yang membungkus sekitar 90 persen dari total kerapatan elektron dalam orbital, seperti yang ditunjukkan pada Gambar (b). Orbital 1s yang ditampilkan dengan cara ini hanyalah bola.
Orbital S
Semua orbital s berbentuk bola tetapi memiliki ukuran berbeda, yang meningkat seiring dengan meningkatnya jumlah kuantum utama. Meskipun detail variasi kerapatan elektron dalam setiap permukaan batas hilang, tidak ada kerugian serius. Bagi kita fitur paling penting dari orbital atom adalah bentuk dan ukuran relatifnya, yang secara memadai diwakili oleh diagram permukaan batas.
Gambar diatas Diagram batas permukaan orbital hidrogen 1s, 2s, dan 3s. Setiap bola mengandung sekitar 90 persen dari total kerapatan elektron. Semua orbital s berbentuk bola. Secara kasar, ukuran orbital sebanding dengan n², di mana n adalah bilangan kuantum utama.
Orbital P
Orbital p mulai dengan bilangan kuantum utama n = 2. Jika n = 1, maka bilangan kuantum momentum sudut 𝓁 hanya dapat mengasumsikan nilai nol; oleh karena itu, hanya ada orbital 1s. Seperti yang kita lihat sebelumnya, ketika 𝓁 = 1, bilangan kuantum magnetik mℓ dapat memiliki nilai -1, 0, 1. Dimulai dengan n = 2 dan 𝓁 = 1, maka kita memiliki tiga orbital 2p: 2px, 2py, dan 2pz (gambar dibawah). Subskrip huruf menunjukkan sumbu sepanjang orientasi orbital. Ketiga orbital p ini identik dalam ukuran, bentuk, dan energi; mereka berbeda satu sama lain hanya dalam orientasi. Diagram batas permukaan orbital p pada Gambar dibawah menunjukkan bahwa setiap orbital p dapat dianggap sebagai dua lobus pada sisi berlawanan dari inti. Seperti orbital s, orbital p bertambah dalam ukuran dari orbital 2p menjadi 3p hingga 4p dan seterusnya.
Gambar diatas merupakan Diagram batas permukaan dari tiga orbital 2p. Orbital-orbital ini memiliki bentuk dan energi yang identik, tetapi orientasinya berbeda. Orbital p dari bilangan kuantum utama yang lebih tinggi memiliki bentuk yang serupa.
Orbital D
Gambar diatas merupakan Diagram batas permukaan dari orbital 3d. Meskipun orbital 3dz² terlihat berbeda, ini setara dengan empat orbital lainnya dalam semua hal lainnya. Orbital d bilangan kuantum utama yang lebih tinggi memiliki bentuk yang serupa
Ketika 𝓁 = 2, ada lima nilai mℓ, yang sesuai dengan lima orbital. Nilai terendah dari n untuk sebuah orbital d adalah 3. Karena 𝓁 tidak pernah bisa lebih besar dari n - 1, ketika n = 3 dan 𝓁 = 2, kita memiliki lima orbital d (3dxy, 3dyz, 3dxz, 3dx²-y², dan 3dz²), ditunjukkan pada Gambar dibawah ini. Seperti dalam kasus orbital p, orientasi orbital d yang berbeda sesuai dengan nilai mℓ yang berbeda, tetapi sekali lagi tidak ada korespondensi langsung antara orientasi yang diberikan dan nilai mℓ tertentu. Semua orbital 3d dalam atom identik dalam energi. Orbital d yang n lebih besar dari 3 (4d, 5d, ...) memiliki bentuk yang serupa.
7.7.1 Energi dari Orbital
Energi elektron dalam atom hidrogen ditentukan semata-mata oleh bilangan kuantum utamanya. Dengan demikian, energi orbital hidrogen meningkat sebagai berikut :
1s < 2s = 2p <3s = 3p = 3d < 4s =4p = 4d = 4f < ...
Energi elektron dalam atom semacam itu tergantung pada jumlah kuantum momentum sudutnya dan juga pada jumlah kuantum utamanya (gambar A). Untuk atom berelektron banyak, tingkat energi 3d sangat dekat dengan tingkat energi 4s. Akan tetapi, energi total atom tidak hanya bergantung pada jumlah energi orbital tetapi juga pada energi tolakan antara elektron-elektron dalam orbital-orbital ini (masing-masing orbital dapat menampung hingga dua elektron. Ternyata energi total atom lebih rendah ketika subkulit 4s dipasang sebelum subkulit 3d. Gambar B menggambarkan urutan orbital atom yang ditempatkan dalam atom berelektron banyak.
Empat bilangan kuantum n, 𝓁, mₗ, dan ms memungkinkan kita memberi label elektron dalam setiap orbital pada atom apa pun. Misalnya, empat bilangan kuantum untuk elektron orbital 2s adalah n = 2, 𝓁 = 0, mₗ = 0, dan ms = -½ atau +½. Sangat tidak nyaman untuk menuliskan semua bilangan kuantum demikian, dan oleh karena itu kita menggunakan notasi yang disederhanakan (n, 𝓁, mₗ, ms). Untuk contoh tersebut, bilangan kuantumnya adalah (2, 0, 0, +½) atau (2, 0, 0, -½). Nilai ms tidak berpengaruh pada energi, ukuran, bentuk, atau orientasi orbital, tetapi menentukan bagaimana elektron diatur dalam orbital.
Atom hidrogen adalah sistem yang sangat sederhana karena hanya mengandung satu elektron. Elektron dapat berada di orbital 1s (keadaan dasar), atau dapat ditemukan di beberapa orbital berenergi lebih tinggi (pada keadaan tereksitasi). Namun, untuk atom berelektron banyak, kita harus mengetahui konfigurasi elektron atomnya, yaitu, bagaimana elektron didistribusikan di antara berbagai orbital atom, untuk memahami sifat elektron. Kita akan menggunakan 10 unsur pertama (hidrogen sampai neon) untuk mengilustrasikan aturan untuk menulis konfigurasi elektron atom di keadaan dasar. Ingatlah bahwa jumlah elektron dalam atom sama dengan nomor atomnya (Z).
Gambar dibawah menunjukkan bahwa elektron dalam atom hidrogen keadaan-dasar harus dalam orbital 1s, sehingga konfigurasi elektronnya adalah 1s¹:
Konfigurasi elektron juga dapat diwakili oleh diagram orbital yang menunjukkan spin elektron :
Panah ke atas menunjukkan salah satu dari dua kemungkinan gerakan spin elektron. (Atau, kita bisa mewakili elektron dengan panah ke bawah.) Kotak mewakili orbital atom.
7.8.1 Prinsip Pengecualian Pauli (Larangan Pauli)
Untuk atom berelektron banyak, kita menggunakan prinsip pengecualian Pauli untuk menentukan konfigurasi elektron. Prinsip ini menyatakan bahwa tidak ada dua elektron dalam atom yang dapat memiliki susunan empat bilangan kuantum yang sama. Jika dua elektron dalam atom memiliki nilai n, 𝓁, dan mₗ yang sama (yaitu, dua elektron ini berada dalam orbital atom yang sama), maka keduanya harus memiliki nilai mₛ yang berbeda. Dengan kata lain, hanya dua elektron yang dapat menempati orbital atom yang sama, dan elektron-elektron ini harus memiliki spin berlawanan. Perhatikan atom helium, yang memiliki dua elektron. Tiga cara yang mungkin untuk menempatkan dua elektron dalam orbital 1s adalah sebagai berikut:
Diagram (a) dan (b) dikesampingkan oleh prinsip pengecualian Pauli. Dalam (a), kedua elektron memiliki putaran ke atas yang sama dan akan memiliki bilangan kuantum (1, 0, 0, +½); dalam (b), kedua elektron memiliki spin ke bawah dan akan memiliki bilangan kuantum (1, 0, 0, -½). Hanya konfigurasi di (c) yang secara fisik dapat diterima, karena satu elektron memiliki bilangan kuantum (1, 0, 0, +½) dan yang lainnya memiliki (1, 0, 0, -½). Dengan demikian, atom helium memiliki konfigurasi sebagai berikut:
Perhatikan bahwa 1s² dibaca "satu s dua," bukan "satu s kuadrat."
7.8.2 Diamagnetisme dan Paramagnetisme
Prinsip pengecualian Pauli adalah salah satu prinsip dasar mekanika kuantum. Prinsip itu bisa diuji dengan observasi sederhana. Jika dua elektron dalam orbital 1s dari atom helium memiliki spin yang sama, atau paralel, (↑↑ atau ↓↓), medan magnet bersihnya akan saling menguatkan [Gambar (a)]. Pengaturan seperti itu akan membuat gas helium paramagnetik. Zat paramagnetik adalah zat yang mengandung spin tidak berpasangan bersih dan tertarik oleh magnet. Di sisi lain, jika elektron berputar berpasangan, atau antiparalel satu sama lain (↑↓ atau ↓↑), efek magnet akan saling membatalkan [Gambar (b)]. Zat diamagnetik tidak mengandung spin tidak berpasangan bersih dan sedikit ditolak oleh magnet.
Pengukuran sifat magnetik memberikan bukti paling langsung untuk konfigurasi elektron unsur tertentu.Melalui percobaan kita menemukan bahwa atom helium dalam keadaan dasarnya tidak memiliki medan magnet bersih. Oleh karena itu, dua elektron dalam orbital 1s harus dipasangkan sesuai dengan prinsip pengecualian Pauli dan gas helium diamagnetik. Aturan yang berguna untuk diingat adalah bahwa setiap atom dengan jumlah elektron ganjil akan selalu mengandung satu atau lebih spin yang tidak berpasangan karena kita membutuhkan jumlah elektron genap untuk pasangan sempurna. Di sisi lain, atom yang mengandung jumlah elektron genap tidak mengandung spin tidak berpasangan. Kita akan segera melihat alasan perilaku ini.
7.8.3 Efek Perisai Pada Atom Berelektron Banyak
Secara eksperimental kita menemukan bahwa orbital 2s terletak pada tingkat energi yang lebih rendah daripada orbital 2p dalam atom berelektron banyak. Gambar dibawah ini menunjukkan plot probabilitas radial untuk orbital 1s, 2s, dan 2p. Karena orbital 2s dan 2p lebih besar dari orbital 1s, sebuah elektron di orbital ini akan menghabiskan lebih banyak waktu jauh dari inti daripada elektron dalam orbital 1s. Dengan demikian, kita dapat mengatakan bahwa elektron 2s atau 2p yang "terperisai" sebagian dari gaya tarik inti oleh elektron 1s. Konsekuensi penting dari efek perisai adalah bahwa ia mengurangi tarikan elektrostatik antara proton dalam inti dan elektron dalam orbital 2s atau 2p.
Melanjutkan diskusi kita tentang atom dari 10 unsur pertama, kita lanjutkan dengan berilium (Z = 4). Konfigurasi elektron keadaan dasar dari berilium adalah 1s²2s², atau
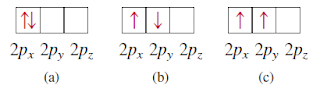
Konfigurasi elektron boron (Z = 5) adalah 1s²2s²2p¹
Perhatikan bahwa elektron yang tidak berpasangan dapat berada dalam orbital 2px, 2py, atau 2pz. Pilihannya sepenuhnya arbitrer karena ketiga orbital p memiliki energi yang setara. Seperti yang ditunjukkan diagram, boron bersifat paramagnetik.
7.8.4 Aturan Hund
Konfigurasi elektron karbon (Z = 6) adalah 1s²2s²2p². Berikut ini adalah cara berbeda untuk mendistribusikan dua elektron di antara tiga orbital p:
Konfigurasi elektron nitrogen (Z = 7) adalah 1s²2s²2p³:
Sekali lagi, aturan Hund menentukan bahwa ketiga elektron 2p memiliki spin paralel satu sama lain; atom nitrogen mengandung tiga elektron tidak berpasangan.
Konfigurasi elektron oksigen (Z = 8) adalah 1s²2s²2p⁴. Atom oksigen memiliki dua elektron yang tidak berpasangan:
Konfigurasi elektron fluor (Z = 9) adalah 1s²2s²2p⁵. Sembilan elektron disusun sebagai berikut:
Atom fluorine memiliki satu elektron yang tidak berpasangan.
Neon (Z=10), subkulit 2p sudah terisi penuh. Konfigurasi elektron neon adalah 1s²2s²2p⁶, dan semua elektron berpasangan, sebagai berikut:
Gas neon harus bersifat diamagnetik, dan pengamatan eksperimental menunjukkan prediksi ini.
7.8.5 Aturan Umum untuk Mengatur Elektron Pada Orbital Atom
Berdasarkan contoh-contoh sebelumnya kita dapat merumuskan beberapa aturan umum untuk menentukan jumlah maksimum elektron yang dapat diatur ke berbagai subkulit dan orbital untuk nilai n:
- Setiap kulit atau tingkat bilangan kuantum utama n berisi n subkulit. Misalnya, jika n = 2, maka ada dua subkulit (dua nilai 𝓁) dari bilangan kuantum momentum sudut 0 dan 1.
- Setiap subkulit dari bilangan kuantum 𝓁 berisi (2𝓁 + 1) orbital. Misalnya, jika 𝓁 = 1, maka ada tiga orbital p.
- Tidak lebih dari dua elektron dapat ditempatkan di setiap orbital. Oleh karena itu, jumlah maksimum elektron hanyalah dua kali lipat jumlah orbital yang digunakan.
- Cara cepat untuk menentukan jumlah elektron maksimum yang dapat dimiliki suatu atom pada tingkat utama n adalah dengan menggunakan rumus 2n².
Pada titik ini mari kita rangkum apa yang telah kita ungkapkan dari sepuluh unsur pertama yang telah diungkapkan tentang konfigurasi elektron keadaan dasar dan sifat-sifat elektron dalam atom:
- Tidak ada dua elektron dalam atom yang sama dapat memiliki empat bilangan kuantum yang sama. Ini adalah prinsip pengecualian Pauli.
- Setiap orbital dapat ditempati oleh maksimal dua elektron. Mereka harus memiliki putaran yang berlawanan, atau bilangan kuantum spin elektron yang berbeda.
- Susunan elektron yang paling stabil dalam subkulit adalah yang memiliki jumlah spin paralel terbanyak. Ini adalah aturan Hund.
- Atom-atom di mana satu atau lebih elektron tidak berpasangan adalah paramagnetik. Atom-atom di mana semua spin elektron berpasangan adalah diamagnetik.
- Dalam atom hidrogen, energi elektron hanya bergantung pada bilangan kuantum utamanya n. Dalam atom berelektron banyak, energi elektron bergantung pada n dan bilangan kuantum momentum sudutnya 𝓁.
- Dalam atom berelektron banyak, subkulitnya diatur dalam urutan yang ditunjukkan pada Gambar 7.21.
- Untuk elektron dengan bilangan kuantum utama yang sama, daya tembusnya, atau kedekatannya dengan inti, berkurang dalam urutan s > p > d > f. Ini berarti bahwa, misalnya, lebih banyak energi diperlukan untuk melepaskan elektron 3s dari atom berelektron banyak daripada yang diperlukan untuk melepaskan elektron 3p.
Konfigurasi elektron semua unsur kecuali hidrogen dan helium diwakili oleh inti gas mulia, yang menunjukkan dalam kurung unsur gas mulia yang hampir mendahului unsur yang sedang dipertimbangkan, diikuti oleh simbol untuk subkulit berlapis tertinggi di kulit terluar. Perhatikan bahwa konfigurasi elektron dari subkulit berlapis tertinggi di kulit terluar untuk unsur-unsur natrium (Z=11) melalui argon (Z=18) mengikuti pola yang mirip dengan yang dari lithium (Z = 3) melalui neon (Z = 10). Konfigurasi elektron kalium (Z = 19) adalah 1s²2s²2p⁶3s²3p⁶4s¹. Karena 1s²2s²2p⁶3s²3p⁶ adalah konfigurasi elektron argon, kita dapat menyederhanakan konfigurasi elektron kalium dengan menulis [Ar] 4s¹, di mana [Ar] menunjukkan “inti argon. ” Demikian pula, kita dapat menulis konfigurasi elektron kalsium (Z = 20) sebagai [Ar] 4s².
Tabel Konfigurasi Unsur-Elektron Keadaan DasarTabel 7.3 Konfigurasi Unsur-Elektron Keadaan Dasar :
Menurut aturan Hund, diagram orbital untuk Cr adalah
Dengan demikian, Cr memiliki total enam elektron tidak berpasangan. Diagram orbital untuk tembaga adalah
Sekali lagi, stabilitas ekstra diperoleh dalam kasus ini dengan memiliki sub kulit 3d sepenuhnya terselesaikan. Secara umum, sub kulit setengah-penuh dan benar-benar berlapis memiliki stabilitas ekstra.
Untuk unsur Zn (Z = 30) hingga Kr (Z = 36), subkulit 4s dan 4p semuanya mudah. Dengan rubidium (Z = 37), elektron mulai memasuki tingkat energi n = 5.
Konfigurasi elektron dalam seri logam transisi kedua [yttrium (Z = 39) menjadi perak (Z = 47)] juga tidak beraturan.
Pengelompokkan unsur sesuai dengan jenis subkulit tempat elektron terluar ditempatkan.
A. Prosedur Percobaan
1. Siapkan Alat dan Bahan yang akan digunakan dengan memilih dan mengambil dari library proteus.
2. Letakkan semua alat dan bahan yang telah diambil ke dalam rangkaian
3. Hubungkan rangkaian tersebut dengan benar
4. Jika telah dihubungkan dengan baik dan benar cobalah rangkaian tersebut
5. Apabila berhasil maka led akan menyala
B. Prinsip Kerja
Rangkaian diatas menggunakan sensor magnet reed switch untuk menggerakkan LED. Pada rangkaian ini menggunakan prinsip pembagi tegangan antara kaki basis transistor. Cara kerja rangkaian adalah jika pada reed switch didekati medan magnet maka hambatan kontak reed switch akan menghubung. Hal ini menyebabkan arus negatif masuk ke kaki transistor, maka transistor tidak akan mengantar arus. Pada saat reed switch dijauhkan dari medan magnet maka kontak reed switch akan membuka, maka arus listrik posistip akan masuk ke kaki basis. Transisotr akan mengalirkan arus negative yang akan menyalakan LED.
Medan magnet dapat menggunakan magnet batang. Contoh aplikasi sederhana adalah indicator atau alarm untuk pintu dibuka atau ditutup.Untuk pengembangan lebih lanjut LED dpat ditambah relay driver untuk mengendalikan alarm atau sirine maupun beban listrik yang lebih besar misalnya lampu AC .
Video>>Klik disini
HTML>>Klik disini
Tidak ada komentar:
Posting Komentar